PAR Transformer XL

An implementation of the Pay-Attention-as-Required Transformer.

For the full project, please follow the link to my github repository: https://github.com/Jmkernes/PAR-Transformer-XL

The PAR Transformer learns which types of layers it prefers. As it trains, you can see it gradually decides what the architecture should be, by choosing between Attention, Dense, or Identity blocks at each layer.

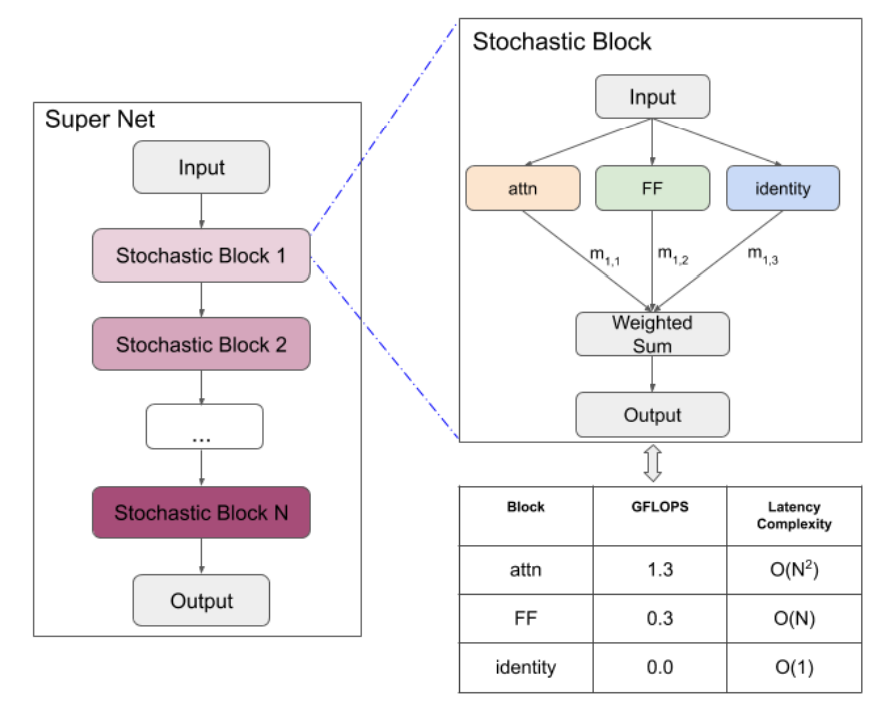
The Pay Attention when Required Transformer (Mandava, et. al. 2020) is just a regular transformer-XL (Dai et. al. 2019), but the ratio of attention and dense layers has been optimized. This optimization is performed by allowing the network to choose which types of layer it prefers in each block of the network. The present implementation is not an exact replica of the author’s efforts. Instead, we perform a simultaneous optimization procedure on both the model architecture and model parameters. The search is performed using a SuperNet, which is a sequential neural network composed of stochastic blocks, as shown in the figure below (taken from the paper. Please don’t sue me!)

A schematic of the superblock layer (Mandava et. al. 2020).

Non-trivial aspects

In order to build a fully functional model, there were several components that we had to build from scratch. These include:

  • An adaptive softmax layer, taken from the paper:
  • The Transformer XL model, which allows one to train long-term dependencies using attention and recurrence: arxiv.
  • A Gumbel-softmax layer, also known as a Relaxed One Hot layer

The Gumbel-softmax

The key component is a Gumbel-Softmax layer (Jang et al., 2016) and (Maddison et al., 2016). This layer is a continuous representation of a discrete sampling from a Categorical distribution, thereby allowing us to use gradients to learn parameters of a discrete distribution. (Recall a categorical is a distrbution over K states with kth state having probability \(\pi_k\), and we must have the normalization condition \(\sum_{i=1}^K \pi_i = 1\))

As the model learns, it is free to adjust both the usual model parameters, as well as its architecture search parameters \(\pi\), indicating the probability of choosing either

  • Attention

  • Dense

  • Identity

for any given stochastic block. We perform simulated annealing: since the categorical distribution is approximated by a continuous representation, we get some scores like (0.02, 0.98, 0.02) for the probability of say sampling that state 2 is picked. The sharpness of this is set by a parameter \(\tau\) (the temperature), with a categorical distribution the limit \(\tau \to 0\). Simulated annealing means we begin with \(\tau=1\) to let the model figure out what it wants, then slowly decrease \(\tau\) so the distribution approaches a categorical.

All of this is implemented on the freely available wiki-text2 dataset.

Explanation of the main GIF

The main gif is the result of our experiments. It shows the \(\pi\) distribution for each stochastic block of a 6 block SuperNet, as a function of training iterations. The number indicates the probability of the most likely layer type (darker means more probable). As you can see, the model learns to put attention in the beginning, and dense layers at the end.

Again, for the full project, please see: https://github.com/Jmkernes/PAR-Transformer-XL